|
[技术]扫雷等式(进阶推理理论基础).精 (27/81935) |
|
|
|
|
作者已重发图片,并引入了新的论证过程。由于字母含义的变动,周彬 (Id:772)的论证过程可能不再准确,敬请谅解。
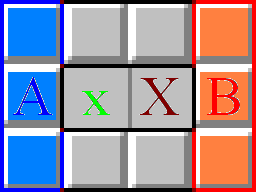
如上图:大X与小x分别代表两个已知的相临数字,周围方块数量设定如下:
A区域方块数为A,B区域方块数为B,A区域雷数为a,B区域雷数为b,公共区域雷数为n
当X=x+B时,B区域方块全是雷,A区域方块全是数。
论证过程:
原假设:x>n ┓
┣ X>n+B ┓
X=x+B ┛ ┣ n+b>n+B → b>B
X=n+b ┛
显然b<=B ∴原假设不成立 → x=n ┓
┣ a=0
x=n+a ┛
x=n ┓
X=x+B ┣ n+B=n+b → B=b
X=n+b ┛
论题得证(以上证明过程不标雷,已经标的雷也当作方块处理)
假如标雷,则应当相应的转换数字的值。
如图:
   
   
   
   
由于图中2的旁边标了一颗雷,要2当成1来看,已经标记的方块也视为已经打开(识别)
根据扫雷等式,可做出如下判断:
   
   
   
   
图中问号方块是数字或者破空,可以点开。
通过扫雷等式,我们还可得出以下推论:
如果两个数字之差=3,那么大数一侧全是地雷,小数一侧全都不是:
   
   
   
   
   
   
两数之差=2时,大数一侧只有在未打开方块数为2时,才可判断:
   
   
   
   
   
   
两数之差=1,且大数一侧只有一颗未打开方块时,形成定式的局面,具体请看张砷镓著《扫雷定式及变化.》
   
   
   
两数之差不可能大于3,为什么不可以,读者可以自己想一想:
   
   
   
这种情况不可能出现。
|
|
最近一次修改:2010-10-17 15:24:07
|
|
|
|
不怎么懂!
能够列多点例子来吗?
|
|
这是一个循环论证,也就是一个错误的证明
主要的问题在于那句“又因为X=公共区域雷数+b→X=x-N+b”
这个“又因为”好像并不是已知条件
事实上只有X=公共区域雷数+B区域雷数(即M)才是已知条件
若那句“又因为”成立,则直接可得到M=b了。下面的证明就没有了任何意义
现证明如下:
为方便比较,所有未知数定义照搬,同时新增L=公共区域雷数
由扫雷程序设定易知:
X=L+M
x=L+N
所以X-x=M-N
而由假设x+b=X可知X-x=b
所以M-N=b
即M-b=N
由扫雷程序设定易知:
b>=(大于等于)M,即M-b<=(小于等于)0
N>=0
所以只有当M-b=0且N=0时,M-b=N才成立
故
M-b=0,即M=b
N=0
命题得证
|
|
|
呵呵,因为是半年前证明出来的,重新修改的时候写的太烦琐,就把自己搞晕啦,谢谢你的指正~!
|
|
多举几个例子吧。看不懂啊。
什么31。。32。。。41。。。。说明白点阿。
我承认我很笨。
|
|
|
高级一直扫得很困难 猜不对 看了几次这扫雷等式 运用后确实有用啊 有点感觉了 终于有些信心了 不再是完全靠运气了 有猜的根据了
|
|
∴原假设不成立 → x=n ┓
这句话不太严密。
因为你的原假设是x>n
原假设不成立,应 → x<=n。
应该加一句:
x=n+a,a>=0 → x>=n
∴ x=n
这样就严密了。
|
|
|
倒不用,因为n肯定不会比x大,n是x旁边的方块,如果超过x就不是扫雷了。
|
|
|
|

